前面的话
假设有一个没有任何排列顺序的电话号码表(或号码簿)。当需要添加联络人和电话时,只能将其写在下一个空位上。假定联系人列表上有很多人,某天,要找某个联系人及其电话号码。但是由于联系人列表没有按照任何顺序来组织,只能逐个检查,直到找到那个想要的联系人为止。想象一下要在黄页上搜寻一个联系人,但是那本黄页没有进行任何组织,那得花多久时间啊?因此,需要组织信息集,比如那些存储在数据结构里的信息。排序和搜索算法广泛地运用在待解决的日常问题中。本文将详细介绍最常用的排序算法
概述
下面创建一个数组(列表)来表示待排序的数据结构
function ArrayList(){ var array = []; //{1} this.insert = function(item){ //{2} array.push(item); }; this.toString= function(){ //{3} return array.join(); };} ArrayList是一个简单的数据结构,它将项存储在数组中(行{1})。只需要一个插入方法来向数据结构中添加元素(行{2}),用JavaScriptArray类原生的push方法即可。最后,为了验证结果,toString方法使用JavaScript原生Array类的join方法,来拼接数组中的所有元素至一个单一的字符串,这样就可以轻松地在浏览器的控制台输出结果了
ArrayList类并没有任何方法来移除数据或插入数据到特定位置。刻意保持简单是为了能够专注于排序算法。所有的排序算法会添加至这个类中
冒泡排序
冒泡算法在所有排序算法中最简单。然而,从运行时间的角度来看,冒泡排序是最差的一个。冒泡排序比较任何两个相邻的项,如果第一个比第二个大,则交换它们。元素项向上移动至正确的顺序,就好像气泡升至表面一样,冒泡排序因此得名
下面来实现一下冒泡排序:
this.bubbleSort = function(){ var length = array.length; //{1} for (var i=0; i array[j+1]){ //{4} swap(j, j+1); //{5} } } }}; 首先,声明一个名为length的变量,用来存储数组的长度(行{1})。这一步可选,它能帮助我们在行{2}和行{3}时直接使用数组的长度。接着,外循环(行{2})会从数组的第一位迭代至最后一位,它控制了在数组中经过多少轮排序(应该是数组中每项都经过一轮,轮数和数组长度一致)。然后,内循环将从第一位迭代至倒数第二位,内循环实际上进行当前项和下一项的比较(行{4})。如果这两项顺序不对(当前项比下一项大),则交换它们(行{5}),意思是位置为j+1的值将会被换置到位置j处,反之亦然
现在声明swap函数(一个私有函数,只能用在ArrayList类的内部代码中):
var swap = function(index1, index2){ var aux = array[index1]; array[index1] = array[index2]; array[index2] = aux;}; 交换时,用一个中间值来存储某一交换项的值。其他排序法也会用到这个方法,因此声明一个方法放置这段交换代码以便重用
下面这个示意图展示了冒泡排序的工作过程:
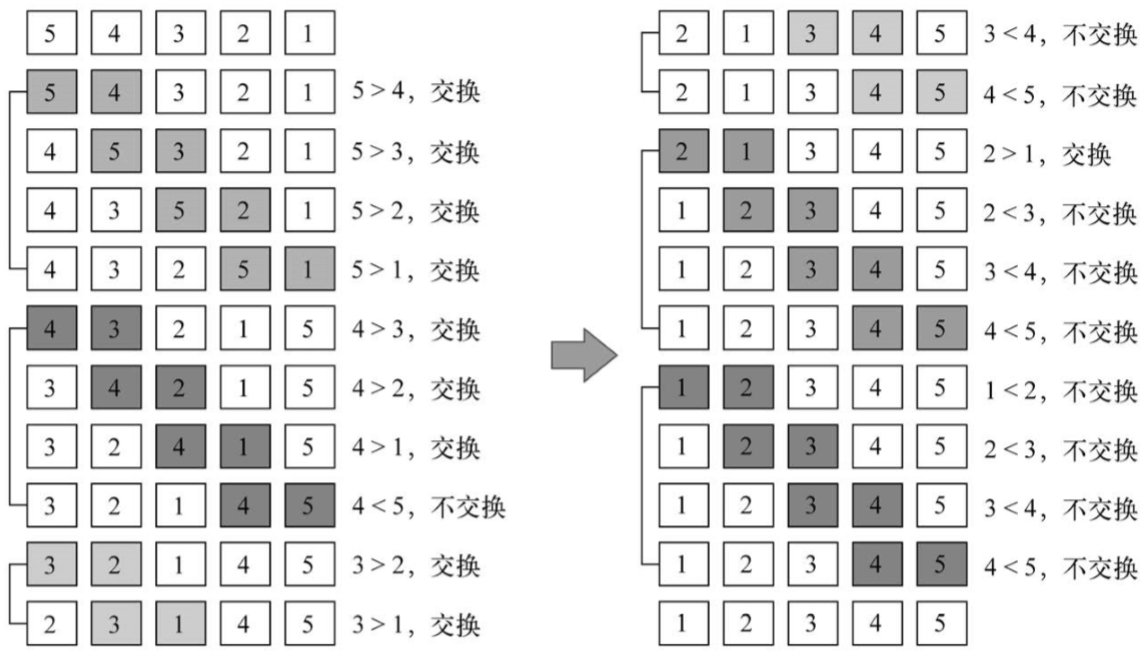
该示意图中每一小段表示外循环的一轮(行{2}),而相邻两项的比较则是在内循环中进行的(行{3})
使用下面这段代码来测试冒泡排序算法,看结果是否和示意图所示一致:
function createNonSortedArray(size){ //{6} var array = new ArrayList(); for (var i = size; i> 0; i--){ array.insert(i); } return array;}var array = createNonSortedArray(5); //{7} console.log(array.toString()); //{8} array.bubbleSort(); //{9} console.log(array.toString()); //{10} 为了测试排序算法,将创建一个函数来自动地创建一个未排序的数组,数组的长度由函数参数指定(行{6})。如果传递5作为参数,该函数会创建如下数组:[5, 4, 3, 2, 1]。调用这个函数并将返回值存储在一个变量中,该变量将包含这个以某些数字来初始化的ArrayList类实例(行{7})。在控制台上输出这个数组内容,确保这是一个未排序数组(行{8}),接着调用冒泡排序方法(行{9})并再次在控制台上输出数组内容以验证数组已被排序了(行{10})
算法执行外循环的第二轮的时候,数字4和5已经是正确排序的了。尽管如此,在后续比较中,它们还一直在进行着比较,即使这是不必要的。因此,可以稍稍改进一下冒泡排序算法
改进后的冒泡排序如下,如果从内循环减去外循环中已跑过的轮数,就可以避免内循环中所有不必要的比较(行{1})
this.modifiedBubbleSort = function(){ var length = array.length; for (var i=0; i array[j+1]){ swap(j, j+1); } } }}; 下面这个示意图展示了改进后的冒泡排序算法是如何执行的:
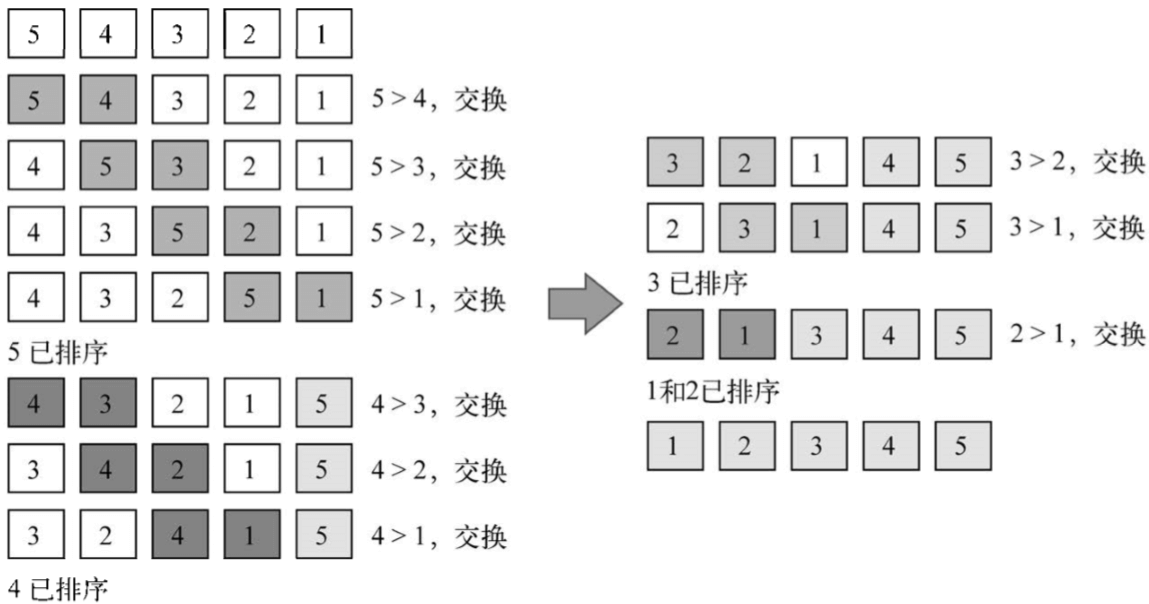
已经在正确位置上的数字没有被比较。即便做了这个小改变,改进了一下冒泡排序算法,但还是不推荐该算法,它的复杂度是O(n2)
选择排序
选择排序算法是一种原址比较排序算法。选择排序大致的思路是找到数据结构中的最小值并将其放置在第一位,接着找到第二小的值并将其放在第二位,以此类推
下面是选择排序算法的代码:
this.selectionSort = function(){ var length = array.length, //{1} indexMin; for (var i=0; i array[j]){ //{5} indexMin = j; //{6} } } if (i !== indexMin){ //{7} swap(i, indexMin); } }}; 首先声明一些将在算法内使用的变量(行{1})。接着,外循环(行{2})迭代数组,并控制迭代轮次(数组的第n个值——下一个最小值)。假设本迭代轮次的第一个值为数组最小值(行{3})。然后,从当前i的值开始至数组结束(行{4}),比较是否位置j的值比当前最小值小(行{5});如果是,则改变最小值至新最小值(行{6})。当内循环结束(行{4}),将得出数组第n小的值。最后,如果该最小值和原最小值不同(行{7}),则交换其值
用以下代码段来测试选择排序算法:
array = createNonSortedArray(5); console.log(array.toString()); array.selectionSort(); console.log(array.toString());
下面的示意图展示了选择排序算法,此例基于之前代码中所用的数组。数组底部的箭头指示出当前迭代轮寻找最小值的数组范围(内循环{4}),示意图中的每一步则表示外循环
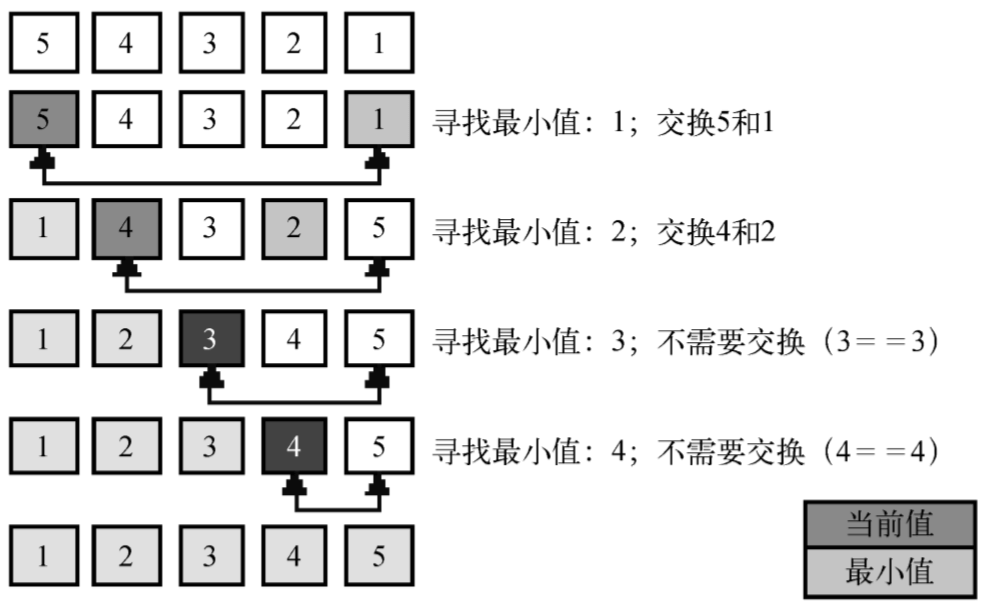
选择排序同样也是一个复杂度为O(n2)的算法。和冒泡排序一样,它包含有嵌套的两个循环,这导致了二次方的复杂度。然而,接下来的插入排序比选择排序性能要好
插入排序
插入排序每次排一个数组项,以此方式构建最后的排序数组。假定第一项已经排序了,接着,它和第二项进行比较,第二项是应该待在原位还是插到第一项之前呢?这样,头两项就已正确排序,接着和第三项比较(它是该插入到第一、第二还是第三的位置呢?),以此类推
下面这段代码表示插入排序算法:
this.insertionSort = function(){ var length = array.length, //{1} j, temp; for (var i=1; i 0 && array[j-1] > temp){ //{5} array[j] = array[j-1]; //{6} j--; } array[j] = temp; //{7} }}; 算法的第一行用来声明代码中使用的变量(行{1})。接着,迭代数组来给第i项找到正确的位置(行{2})。注意,算法是从第二个位置(索引1)而不是0位置开始的(我们认为第一项已排序了)。然后,用i的值来初始化一个辅助变量(行{3})并将其值亦存储于一临时变量中(行{4}),便于之后将其插入到正确的位置上。下一步是要找到正确的位置来插入项目。只要变量j比0大(因为数组的第一个索引是0——没有负值的索引)并且数组中前面的值比待比较的值大(行{5}),就把这个值移到当前位置上(行{6})并减小j。最终,该项目能插入到正确的位置上
下面的示意图展示了一个插入排序的实例:

假定待排序数组是[3, 5, 1, 4, 2]。这些值将被插入排序算法按照下面形容的步骤进行排序
1、3已被排序,所以我们从数组第二个值5开始。3比5小,所以5待在原位(数组的第二位)。 3和5排序完毕
2、下一个待排序和插到正确位置上去的值是1(目前在数组的第三位)。5比1大,所以5被移至第三位去了。我们得分析1是否应该被插入到第二位——1比3大吗?不,所以3被移到第二位去了。接着,我们得证明1应该插入到数组的第一位上。因为0是第一个位置且没有负数位,所以1必须被插入到第一位。1、3、5三个数字已经排序
3、4应该在当前位置(索引3)还是要移动到索引较低的位置上呢?4比5小,所以5移动到索引3位置上去。那么应该把4插到索引2的位置上去吗?4要比3大,所以4插入到数组的位置3上
4、下一个待插入的数字是2(数组的位置4)。5比2大,所以5移动至索引4。4比2大,所以4也得移动(位置3)。3也比2大,所以3还得移动。1比2小,所以2插入到数组的第二位置上。至此,数组已排序完成
排序小型数组时,此算法比选择排序和冒泡排序性能要好
归并排序
归并排序是第一个可以被实际使用的排序算法。前三个排序算法性能不好,但归并排序性能不错,其复杂度为O(nlogn)
归并排序是一种分治算法。其思想是将原始数组切分成较小的数组,直到每个小数组只有一个位置,接着将小数组归并成较大的数组,直到最后只有一个排序完毕的大数组
由于是分治法,归并排序也是递归的:
this.mergeSort = function(){ array = mergeSortRec(array);}; 每当要实现一个递归函数,要实现一个实际被执行的辅助函数。声明mergeSort方法以供随后使用,而mergeSort方法将会调用mergeSortRec,该函数是一个递归函数:
var mergeSortRec = function(array){ var length = array.length; if(length === 1) { //{1} return array; //{2} } var mid = Math.floor(length / 2), //{3} left = array.slice(0, mid), //{4} right = array.slice(mid, length); //{5} return merge(mergeSortRec(left), mergeSortRec(right)); //{6}}; 归并排序将一个大数组转化为多个小数组直到只有一个项。由于算法是递归的,需要一个停止条件,在这里此条件是判断数组的长度是否为1(行{1})。如果是,则直接返回这个长度为1的数组(行{2}),因为它已排序了
如果数组长度比1大,那么我们得将其分成小数组。为此,首先得找到数组的中间位(行{3}),找到后我们将数组分成两个小数组,分别叫作left(行{4})和right(行{5})。left数组由索引0至中间索引的元素组成,而right数组由中间索引至原始数组最后一个位置的元素组成。
下面的步骤是调用merge函数(行{6}),它负责合并和排序小数组来产生大数组,直到回到原始数组并已排序完成。为了不断将原始数组分成小数组,得再次对left数组和right数组递归调用mergeSortRec,并同时作为参数传递给merge函数
var merge = function(left, right){ var result = [], // {7} il = 0, ir = 0; while(il < left.length && ir < right.length) { // {8} if(left[il] < right[ir]) { result.push(left[il++]); // {9} } else{ result.push(right[ir++]); // {10} } } while (il < left.length){ // {11} result.push(left[il++]); } while (ir < right.length){ // {12} result.push(right[ir++]); } return result; // {13} }; merge函数接受两个数组作为参数,并将它们归并至一个大数组。排序发生在归并过程中。 首先,需要声明归并过程要创建的新数组以及用来迭代两个数组(left和right数组)所需的两个变量(行{7})。迭代两个数组的过程中(行{8}),比较来自left数组的项是否比来自right数组的项小。如果是,将该项从left数组添加至归并结果数组,并递增迭代数组的控制变量(行{9});否则,从right数组添加项并递增相应的迭代数组的控制变量(行{10})。接下来,将left数组或者right数组所有剩余的项添加到归并数组中。最后,将归并数组作为结果返回
如果执行mergeSort函数,下图是具体的执行过程:
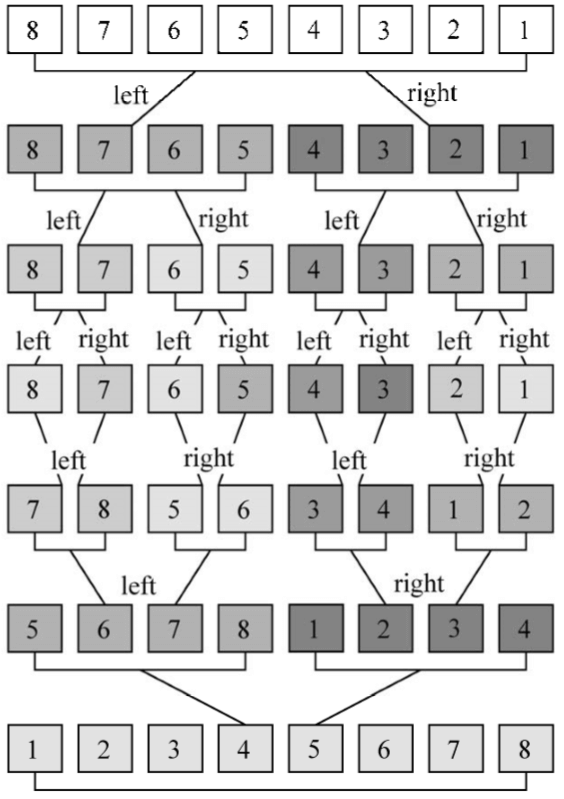
算法首先将原始数组分割直至只有一个元素的子数组,然后开始归并。归并过程也会完成排序,直至原始数组完全合并并完成排序
快速排序
快速排序也许是最常用的排序算法了。它的复杂度为O(nlogn),且它的性能通常比其他的复杂度为O(nlogn)的排序算法要好。和归并排序一样,快速排序也使用分治的方法,将原始数组分为较小的数组(但它没有像归并排序那样将它们分割开)
1、首先,从数组中选择中间一项作为主元
2、创建两个指针,左边一个指向数组第一个项,右边一个指向数组最后一个项。移动左指针直到我们找到一个比主元大的元素,接着,移动右指针直到找到一个比主元小的元素,然后交换它们,重复这个过程,直到左指针超过了右指针。这个过程将使得比主元小的值都排在主元之前,而比主元大的值都排在主元之后。这一步叫作划分操作
3、接着,算法对划分后的小数组(较主元小的值组成的子数组,以及较主元大的值组成的子数组)重复之前的两个步骤,直至数组已完全排序
下面来实现快速排序
this.quickSort = function(){ quick(array, 0, array.length - 1);}; 就像归并算法那样,开始声明一个主方法来调用递归函数,传递待排序数组,以及索引0及其最末的位置(因为我们要排整个数组,而不是一个子数组)作为参数
var quick = function(array, left, right){ var index; //{1} if (array.length > 1) { //{2} index = partition(array, left, right); //{3} if (left < index - 1) { //{4} quick(array, left, index - 1); //{5} } if (index < right) { //{6} quick(array, index, right); //{7} } }}; 首先声明index(行{1}),该变量能帮助我们将子数组分离为较小值数组和较大值数组,这样,就能再次递归的调用quick函数了。partition函数返回值将赋值给index(行{3})
如果数组的长度比1大(因为只有一个元素的数组必然是已排序了的(行{2}),我们将对给定子数组执行partition操作(第一次调用是针对整个数组)以得到index(行{3})。如果子数组存在较小值的元素(行{4}),则对该数组重复这个过程(行{5})。同理,对存在较大值得子数组也是如此,如果存在子数组存在较大值,我们也将重复快速排序过程(行{7})
现在来看看划分过程:
var partition = function(array, left, right) { var pivot = array[Math.floor((right + left) / 2)], //{8} i = left, //{9} j = right; //{10} while (i <= j) { //{11} while (array[i] < pivot) { //{12} i++; } while (array[j] > pivot) { //{13} j--; } if (i <= j) { //{14} swapQuickStort(array, i, j); //{15} i++; j--; } } return i; //{16} }; 第一件要做的事情是选择主元(pivot),有好几种方式。最简单的一种是选择数组的第一项(最左项)。然而,研究表明对于几乎已排序的数组,这不是一个好的选择,它将导致该算法的最差表现。另外一种方式是随机选择一个数组项或是选择中间项。在本实现中,我们选择中间项作为主元(行{8})。初始化两个指针:left(低——行{9}),初始化为数组第一个元素;right(高——行{10}),初始化为数组最后一个元素
只要left和right指针没有相互交错(行{11}),就执行划分操作。首先,移动left指针直到找到一个元素比主元大(行{12})。对right指针,做同样的事情,移动right指针直到找到一个元素比主元小
当左指针指向的元素比主元大且右指针指向的元素比主元小,并且此时左指针索引没有右指针索引大(行{14}),意思是左项比右项大(值比较)。交换它们,然后移动两个指针,并重复此过程(从行{11}再次开始)
在划分操作结束后,返回左指针的索引,用来在行{3}处创建子数组
swapQuickStort函数和swap函数十分相似。唯一的不同之处是发生交换值的的数组同样也是函数的参数
var swapQuickStort = function(array, index1, index2){ var aux = array[index1]; array[index1] = array[index2]; array[index2] = aux;}; 下面来一步步地看一个快速排序的实际例子:
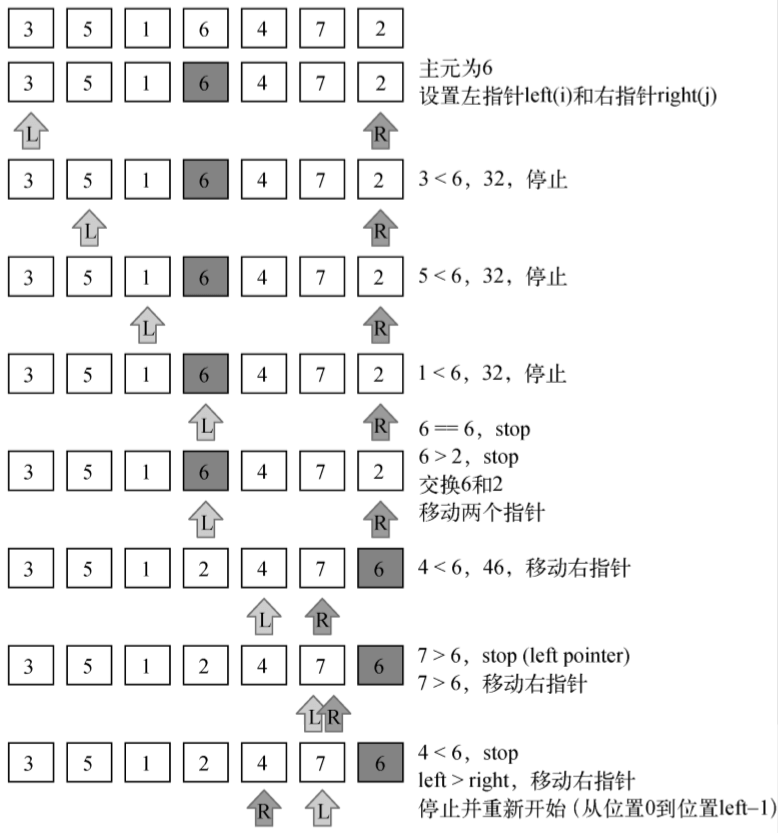
给定数组[3, 5, 1, 6, 4, 7, 2],前面的示意图展示了划分操作的第一次执行。
下面的示意图展示了对有较小值的子数组执行的划分操作(注意7和6不包含在子数组之内):

接着,继续创建子数组,请看下图,但是这次操作是针对上图中有较大值的子数组(有1的那个较小子数组不用再划分了,因为它仅含有一个项)
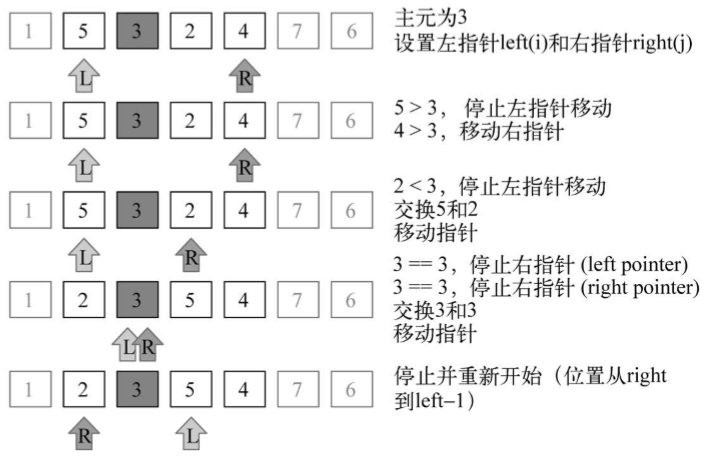
子数组([2, 3, 5, 4])中的较小子数组([2, 3])继续进行划分(算法代码中的行{5}):
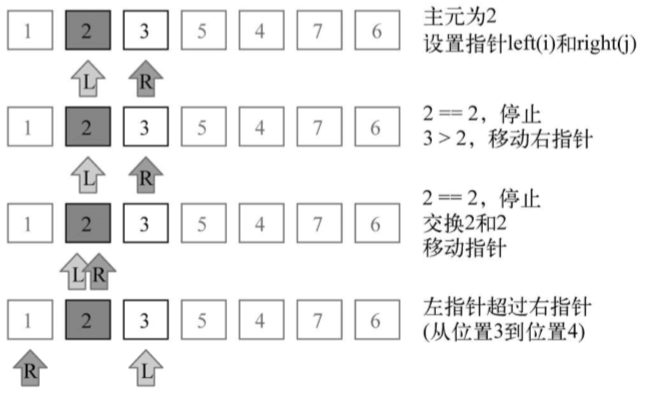
然后子数组([2, 3, 5, 4])中的较大子数组([5, 4])也继续进行划分(算法中的行 {7}),示意图如下:

最终,较大子数组[6, 7]也会进行划分(partition)操作,快速排序算法的操作执行完成
堆排序
堆排序也是一种很高效的算法,因其把数组当作二叉树来排序而得名。这个算法会根据以下信息,把数组当作二叉树来管理
索引0是树的根节点除根节点外,任意节点N的父节点是N/2; 节点L的左子节点是2*L 节点R的右子节点是2*R+1
举例来说,可以将数组[3, 5, 1, 6, 4, 7, 2]想象成下面的树:
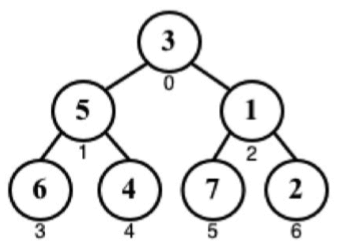
堆排序算法实现如下:
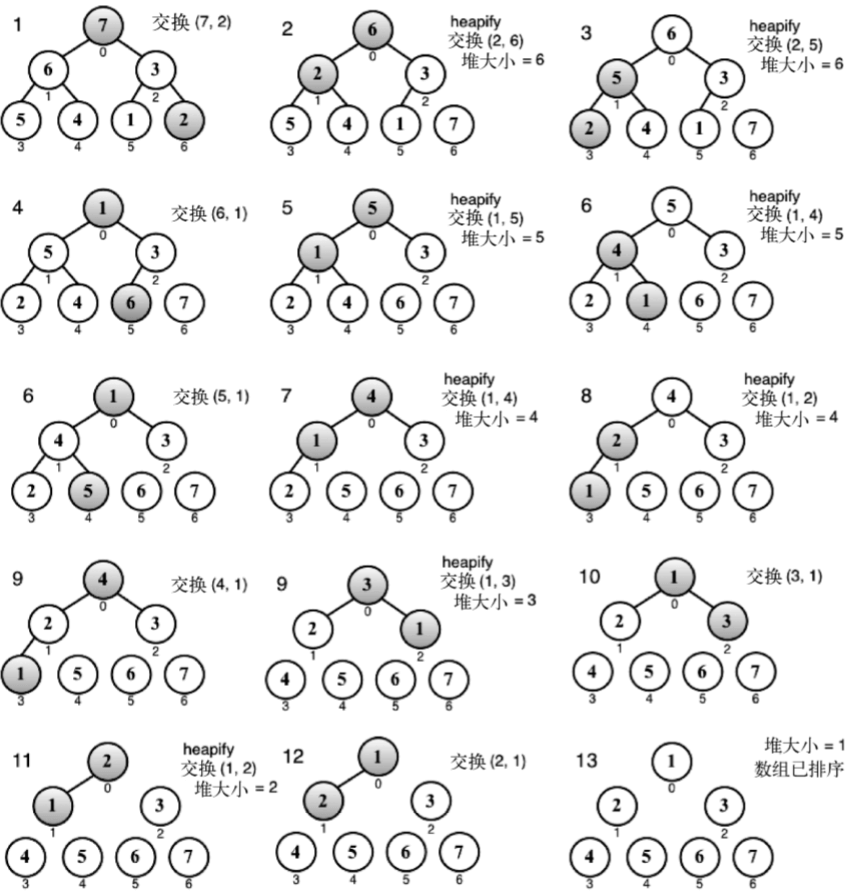
this.heapSort = function() { var heapSize = array.length; buildHeap(array); //{1} while (heapSize > 1) { heapSize--; swap(array, 0, heapSize); //{2} heapify(array, heapSize, 0); //{3} } }; 第一步,构造一个满足array[parent(i)] ≥ array[i]的堆结构(行{1})
第二步,交换堆里第一个元素(数组中较大的值)和后一个元素的位置(行{2})。这样, 大的值就会出现在它已排序的位置。
第二步可能会丢掉堆的属性。因此,我们还需要执行一个heapify函数,再次将数组转换成堆,也就是说,它会找到当前堆的根节点(较小的值),重新放到树的底部。
buildHeap函数实现如下:
var buildHeap = function(array){ var heapSize = array.length; for (var i = Math.floor(array.length / 2); i >= 0; i--) { heapify(array, heapSize, i); } }; 如果对数组[3, 5, 1, 6, 4, 7, 2]调用buildHeap函数,堆的构建过程如下:
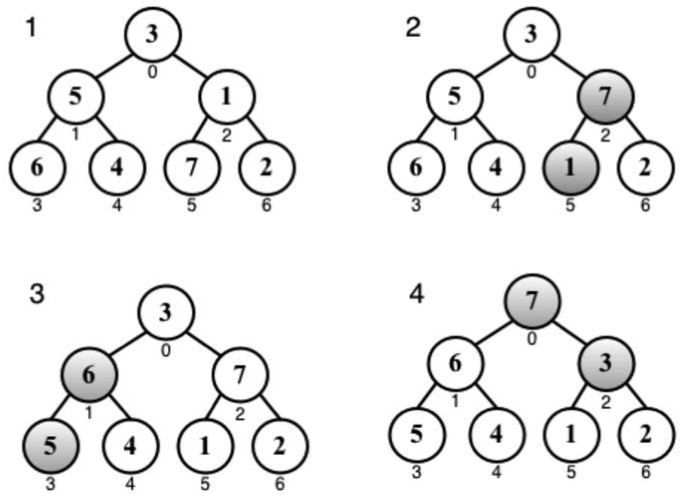
heapify函数实现如下:
var heapify = function(array, heapSize, i){ var left = i * 2 + 1, right = i * 2 + 2, largest = i; if (left < heapSize && array[left] > array[largest]) { largest = left; } if (right < heapSize && array[right] > array[largest]) { largest = right; } if (largest !== i) { swap(array, i, largest); heapify(array, heapSize, largest); }}; 堆构造好之后,就可以应用堆排序的算法了,也就是行{2}和行{3}